R7年度　騒音・振動特論　問5

問5

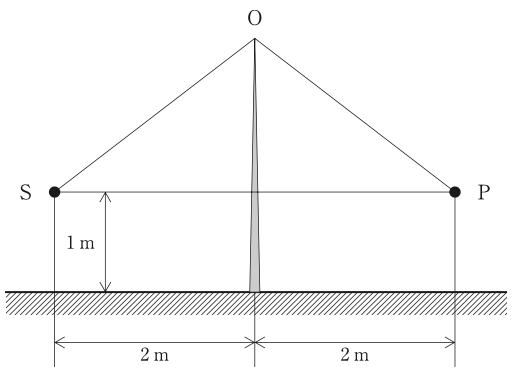
工場内の機械に，周波数1020Hzの純音性の騒音を発する全指向性点音源Sがある。点音源Sと測定点Pとの間には，下図のように高さ2.5mの塀(地表面から頂点Oまでの高さ)が設置されている。測定点Pでの騒音レベルを低減する必要が生じたことから，塀の高さを5mに変更することを計画している。この変更により，騒音レベルは約何dB低減するか。ただし，塀の長さは十分に長く，また，塀からの透過音及び地表面での反射音は無視できるものとする。音速を340m/s，√5=2.24として計算せよ。

(1)　7

(2)　10

(3)　13

(4)　16

(5)　19

解答

(1)

解説

本問題は下記公式を用いて，塀の高さを変更する前後の減衰量を求めます。

R=10logN+13　ここでN=σ/(λ/2)とし，σは距離差，λは波長とします。

変更前の定数をそれぞれN1，R1等とすると，

\(σ1=SO1+OP1-SP\)

\(SO1=OP1=\sqrt{2^{2}+1.5^{2}}=\sqrt{6.25}=2.5\)

よって，σ1は下記の通りとなります。

\(σ1=2.5+2.5-4=1\)

今回周波数1020Hzのため，波長λは，

\(λ=340/1020=1/3\)　と求まります。これまでに求めた各定数を公式に当てはめると，

\(N1=σ1/(λ/2)=1/(1/6)=6\)

\(R1=10logN1+13=10log6+13=10・0.77+13=20.7dB\)

同様に変更後のR2も求めます。

\(σ2=SO2+OP2-SP\)

\(SO2=OP2=\sqrt{2^{2}+4^{2}}=\sqrt{20}=2\sqrt{5}=4.48\)

\(σ2=4.48+4.48-4=4.96\)

\(N2=σ2/(λ/2)=4.96/(1/6)=29.76≒30\)

\(R2=10logN2+13=10log30+13\\
\hspace{8mm}=10log3+10log10+13=10・0.47+10+13=27.7dB\)

よって，R1とR2の差は7dBと分かります。