問25
図(a)のばね定数kのばね4個で質量mを支持する1自由度振動系で表すことのできる機械を,図(b)のばね定数2kのばねで9個で質量2mを支持する機械に入れ替えた場合,(b)の固有振動数は,(a)の固有振動数のおよそ何倍になるか。
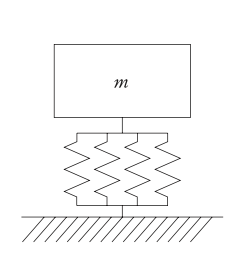
(a)
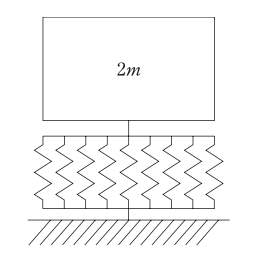
(b)
| (1) 1.25 | (2) 1.5 | (3) 1.75 | (4) 2 | (5) 2.25 |
解答
(2)
解説
本設問は下記公式より求めます。
\(ω=\sqrt {\large \frac{k}{m}}\)また,ばね定数は今回の図では並列に接続されているため,合計定数はその和となります。
これらを代入すると図(a)においては,
図(b)も同様に,
\(ω_{b}=\sqrt {\large \frac{2k×9}{2m}} = \sqrt {\large \frac{9k}{m}}\)最終的に今回求めたいのは,(b)の固有振動数は(a)の何倍か,であるため下記にそれぞれ代入して,xを求めます。
\(ω_{b}=ω_{a}×x\)それぞれ代入すると,
\(\sqrt {\large \frac{9k}{m}}=\sqrt {\large \frac{4k}{m}}×x\) \(3\sqrt {\large \frac{k}{m}}=2\sqrt {\large \frac{k}{m}}×x\) \(3=2×x\)よって,最終的にはx = 1.5と求まります。


コメント